
Using attractors for evolution
Complexity theory tells us that dynamic complex systems can settle into any of many possible different steady states - depending upon the values of the system variables. These steady states are called 'attractor basins' or more simply 'attractors'. Changing the variables associated with a system can cause it to switch from one attractor basin (steady state) to another.
On the face of it, this seems to offer no possibility for controlling the state of a dynamic complex system because attractor states occur unpredictably. However, this conceptual model of a dynamic complex system (settling into attractor states) provides us with an insight into how they work, allowing us to define our own attractor states.
It doesn't seem logical that on the one hand the steady states are unpredictable, yet, on the other hand, we can choose our own.
This paradox is resolved if you consider all the possible steady states that a system can settle into. Some states will be satisfactorty, others will not. Defining a suitable state means altering the variables until the system settles into a particular state that happens to be suitable.
In other words, you define your own attractor by specifying what kind of steady state you are looking for: what rules you want it to obey. Then you can keep disturbing the system until it happens to settle into a particular stae that obeys the rules you have specified.
This can be likened to choosing the right leader for a team. The team will perform differently according to which team member is the leader. One particular choice will be the best and you can find out which by trying out different leaders and choosing the one that causes the team to work most efficiently.
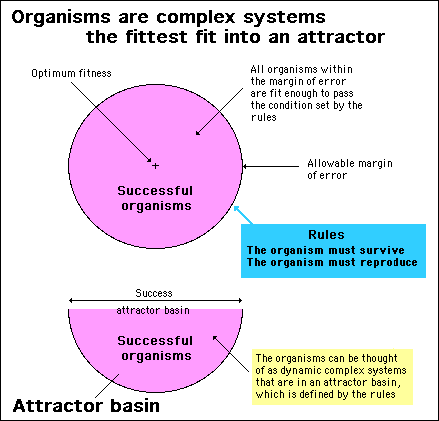
Any living organism - which is effectively a complex dynamic system - can be in a state of success in evolutionary terms, or, in a state of failure. As far as complexity theory is concerned, these two states are attractors of the system - where the organism can be in either one or another. The figure below shows how the margin of error of an organism's design can be represented as an attractor basin in complexity theory.
Attractors as control elements
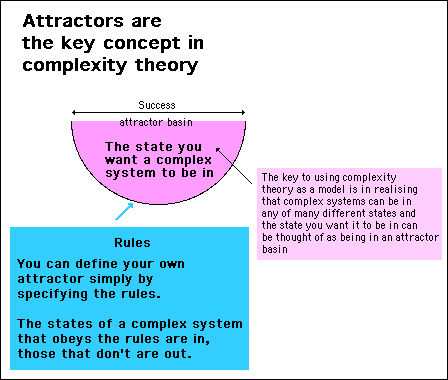
What this implies is that we can arbitrarily set rules to define a system state and this will effectively become a system attractor. Any state of the system conforming to the rules is in the attractor; any state that doesn't is outside of the attractor.
Here is a mechanism we can use to control a complex system. We can play around with a system's variables until it flips into an attractor state we have defined as illustrated in the diagram below.
This approach can be applied to any dynamic complex system
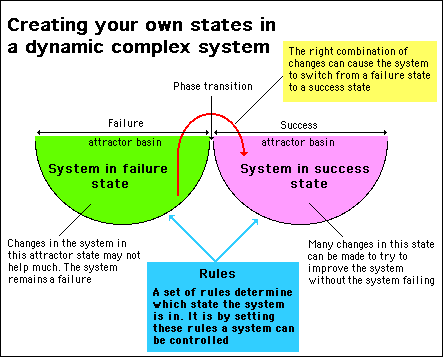
There is no reason why the defining of states, or attractors, shouldn't be applied to any dynamic system. It can be applied to the design of a system that involves human behavior, particularly to systems where humans are collaborating.
In this instance, we shall be using these principles as the basis for controlling the performance of stigmergic systems. Where a complete system consists of: Web sites; visitors to Web sites; the people who make changes to Web sites; the people who provide information that appears on Web sites; competition; search engines; the current stage of computer technology; the whole of the World Wide Web and the Internet.
Summary
What chaos theory and the idea of attractors does for us is to provide a unique mindset for dealing with complex situations. It doesn't provide algorithmic solutions. It tells us that we have to have systems that can be easily and quickly re-configured and changed.
We don't have to worry about coming up with an optimum system design from the beginning. The optimum design will emerge as a consequence of an evolutionary strategy.
End of article