
A small world
The significance
The significance of the Kevin Bacon game wasn't truly appreciated until, Duncan Watts and Steven Strogatz, at Cornell University in Ithaca, New York, worked on a project to analyze complex networks. This work was written up and published in the eminent journal NATURE under the title "Collective dynamics of 'small-world' networks" (volume 393, pp. 440-442 , 4 June 1998). This paper attracted considerable world wide attention.
At that time, networks were considered to act in two possible ways:
1) As a network of local connections:
This involves a system of nodes where every node is connected directly to a relatively small number of neighboring nodes. Communications can then take any route through the network of nodes – raveling from one node to the next.
This can be likened to a large hall full of people. The people in the hall are not allowed to shout and there is no broadcasting or telephone system: they can only speak to the people who are immediately next to them. Information and messages can then only pass between people in different parts of the hall by means of a series of intermediate links. One person telling a person near to them, who then tells another person near to them, who tells yet another person near to them, and so on until a message passes from one person to another via all the links between the original sender and a destination receiver.
As each person is surrounded by several others, they have many alternative choices as to which of the people next to them they pass a message on to. Indeed, the message can be simultaneously passed to several people standing next to them, allowing many copies of the same message to take different routes through the people in the hall to reach an intended recipient.
Conversely, the recipient, of any message coming from somebody in another part of the hall, can receive the message from any of the people standing near to them, depending upon which route the message took as it passed from person to person on its way from the original sender. It is in this way that many people think of information spreading by word of mouth – the spreading of rumor's in a community of people might be a good example.
The problem with this type of network is that it can easily become saturated with messages unless the messages are accompanied by a specific address. It is only truly efficient if the route from one person to another is specified beforehand and sent with the message.

Figure 2 - A normal network, showing each node connecting to eight neighbors. Messages can flow from one node to any other node in the network via multiple different pathways
Figure 2 illustrates a typical normal network. This network is such that every node is connected to eight other nodes. As you can see by tracing paths through the network of connections, a message can be sent to any other node by a variety of different routes. This diagram might represent a town full of people where each person is restricted to talking only to eight of their immediate nearest neighbors; it can readily be seen how information (and gossip) can spread around this community in an extremely large number of different ways.
The disadvantage of a normally connected network is that it can take a large number of steps, or links, to get from one part of the network to another. For this reason a network of random connections is often preferred.
2) As a network of random connections:
This is a system of network connections whereby each node is connected to a relatively small number of other nodes that are randomly distributed around a network. The efficiency of the network is determined by the least number of nodes the communication has to pass through as it passes from a starting node to a finishing node.
This can be imagined as a country full of people at home with a telephone. Each of them is given a small list of telephone numbers of people randomly distributed around the country. Figure 3 illustrates three such people, each of which has eight random connections to other people who can be located anywhere in an environment.
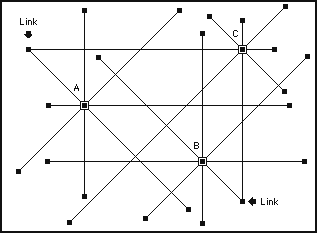
Figure 3 - A random network, showing just three people (A, B and C) who are each connected randomly to eight others around the country. Notice how they can share people – link nodes – which has a dramatic effect on the number of steps it takes to transfer information from any part of the network to another. In this case, a maximum of four steps from any one node to another
Because every person is connected to several others, each can be considered to be within a small cluster of people in the same way that an actor or actress can be considered to be within a small cluster of actors and actresses when they make a film. Just as Bacon numbers are calculated by looking for the least number of links between actors and actresses across films, so the efficiency of a randomly connected network is calculated by calculating the least number of links it takes to pass a message from one node (person on a telephone) to another.
In figure 3, it can be seen how just a couple of common nodes between clusters can effectively connect people together in a short number of steps. This is why Bacon numbers can be so small, even when actors and actresses may not even have been working in the same decade as each other. All it takes is for one common actor or actress to span a decade, to create a link for thousands of others.
The advantage of a random network over a normal network is that, as long as there are at least a few common links, the number of links between nodes is very small. This is true however many nodes there are in the network. This is why the average number of links between actors and actresses in all films made can be as low as three, even though there are hundreds of thousands of actors and actresses.