
The surprise
Duncan Watts and Steven Strogatz's discovery came about when they simulated various kinds of networks between the extremes of a locally connected network and a randomly connected network. This can be explained in terms of all the people in the hall as previously described, but, a few of them having mobile telephones that enables them to pass a message to somebody in a distant part of the hall. This is illustrated in figure 4, where small local clusters contain at least one node that has a random connection to a distant node.
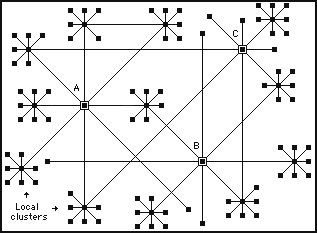
Figure 4 - Local clusters mixed with random links
Effectively, the kind of computer simulations Watts and Strogatz analyzed on their computer was to see how the average minimum number of links needed, to transfer messages between any pair of people, was affected by the proportion of people who had mobile phones. If nobody had a mobile phone, the system would represent a locally connected network. If they all had mobile phones the system would represent a randomly connected network. Watts and Strogatz wanted to find out how the efficiency (minimum number of links between sender and target recipient) varied between these two extremes.
Computer simulations showed that randomly connected networks needed far fewer links to connect to nodes than locally connected networks. The surprise came when they started adding random links to the locally connected network. Instead of the network slowly becoming more efficient, as more and more links were changed from local to random, they found the efficiency jumped up to near the efficiency of a randomly connected network as soon as only a very small number of nodes were randomly connected.
These simulations can be visualized by again imagining the hall full of people. Then, a probability number is used to decide whether or not each person gets to have a mobile phone (complete with a small list of the telephone numbers of other people randomly distributed around the hall). A probability of 1 will give everyone a mobile phone, a probability of 0 will give nobody a mobile phone. Applying a probability of 0.1 to each person (one chance in ten) will give about one in ten of them a phone and a probability of 0.8 will give about eighty percent of them a phone.
The simulations start with a very small probability (say, .01 – where only one in a hundred get a mobile phone and a small list of numbers) and calculating the average number of links needed to transfer messages between different pairs of people. Then this calculation is repeated again and again as the probability is slowly increased (and more people have phones). They then plot a graph to show how the efficiency (minimum number of links to transfer messages between people) changes with the change in the number of people who have mobile phones.
The results showed that if only a few random links are placed into the network (just a few people have mobile phones) the efficiency, or least number of links between nodes, is almost the same as if all the connections were random (everyone having a mobile phone).
This is like saying that message passing between a hall full of people - where only a few of them have mobile phones (each with a limited list of the numbers of other people in the hall) - is almost as efficient as if everyone in the hall had a mobile phone (each with a limited list of the numbers of other people in the hall). This was an unexpected result – causing great surprise because it is counter intuitive.